定义

在计算机科学中，时间复杂性，又称时间复杂度，算法的时间复杂度是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。

常见复杂度说明

复杂度	说明
1	大部分程序的部分指令只执行一次，或最多几次，如果一个程序的所有指令具有这样的性质，那么这个程序的执行时间是常数
logN	如果一个程序的运行时间是对数级的，则随着N的增大会渐渐慢下来，如果一个程序将一个大的问题分成一系列更小的问题，每一步都将问题的规模缩小成几分之一。一般就会出现这样的运行时间函数，在我们所关心的范围内，可以认为运行时间小于一个大的常数。 对数的基数会影响这个常数，但是影响不会太大，当N=1000时，如果基数是10，logN等于3；如果基数是2，logN约等于10，当N=100000，logN只是前值的两倍，logN只增长了一个常数因子；仅当从N增长到N平方时，logN才会增长到原来的两倍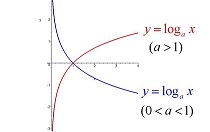
N	如果程序的运行时间是线性的，很可能是这样的情况：对每个输入的元素都做了少量的处理，当N=1000000时，运行时间大概也是这个数值；当N增长到原来的两倍时，运行时间大概也增长了原来的两倍，如果一个算法必须处理N个输入（或者产生N个输出），这种情况是最优的
NlogN	如果某个算法将问题分解成更小的子问题。独立的解决各个子问题，最终把结果综合起来（如归并排序，堆排序），运行时间一般就是NlogN，当N=1000000时，NlogN大约就是2000000，当N增长到原来的两倍，运行时间超过原来的两倍，但是超过不是太多
N平方	如果一个算法的时间是二次方，那么它一般只能用于一些规模小的问题，这样的运行时间通常存在于需要处理每一对输入数据项的算法（在程序中很可能表现为一个嵌套循环）中，当N=1000时，运行时间是1000000；
N三次方	类似的，如果一个算法需要处理输入数据想的三元组（很可能表现为三重嵌套循环），其运行时间一般就是三次的，只能用于一些规模较小的问题。当N=100时，运行时间就是1 000 000；如果N增长到原来的两倍，运行时间将会增长到原来的八倍
2的N次方	如果一个算法的运行时间是指数级的（exponential），一般它很难在实践中使用，即使这样的算法通常是对问题的直接求解。当N=20时，运行时间是1 000 000；如果增长到原来的两倍时，运行时间将是原时间的平方