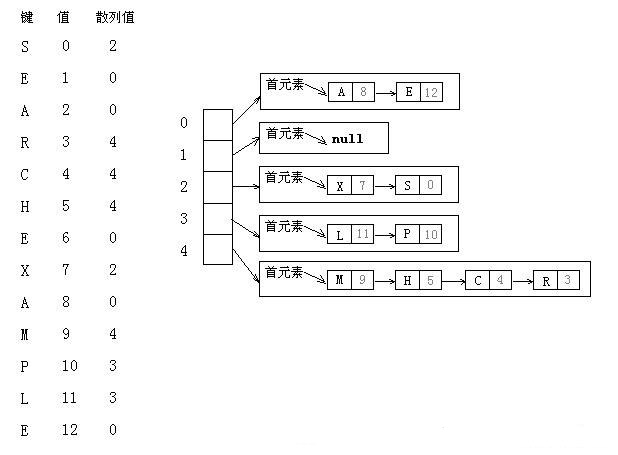
介绍

如果所有的键都是小整数，我们可以用一个数组来实现无序的符号表，将健作为数组的索引而且数组中键i处存储的就是他对应的值。这样我们就可以快速访问任意键的值。

散列表就是这种简易方法的扩展并能够处理更加复杂的类型的键，需要用算术操作将键转化为数组的索引来访问数组中的键值对。

散列表是算法在时间和空间上做出权衡的例子，如果没有内存限制，我们可以直接将键作为（可能是一个超大的）数组的索引，那么所有查找操作只需要访问内存一次就可以完成。但这种理想的情况不会经常出现，因为当键很多时候需要的内存太大。另一方面。如果没有时间限制，我们可以使用无序数组并进行顺序查找，这样就只需要很少的内存，而散列表使用了适度的空间和时间并在这两种极端之间找到了一种平衡。

使用散列表，可以实现在一般应用中拥有（均摊后）常数级别的查找和插入操作的符号表。

步骤

使用散列的查找算法分成两步：

• 第一步：使用散列函数将被查找的键转化成数组的一个索引。

• 第二步：处理碰撞冲突的过程。理想情况下，不同的键都能转化成不同的索引值。但实际上，我们需要面对两个或者多个键都会散列到相同的索引值的情况。主要有两种解决碰撞的方法：拉链法和线性探测法。

散列函数

在散列函数的计算这个过程中，会将键转化成数组的索引。如果我们有一个能够保存M个键值对的数组，那么我们就需要一个能够将任意键转化为该数组范围内的索引（[0,M-1]范围内的整数）的散列函数，我们要找的散列函数应该易于计算并且能够均匀分布所有的键，即对于任意键，0到M-1之间的每个整数都有相等的可能性与之对应（与键无关）

散列函数和键的类型有关。严格来说，对于每种类型的键我们都需要一个与之对应的散列函数:

正整数：将整数散列常用的方法是除留余数法。选择大小为素数M的数组，对于任意正整数k，计算k除以M的余数。这个函数的计算非常容易（在java中为k%M）并能够有效的将键散步在0到M-1范围内，如果M不是素数，我们可能无法利用键中包含的所有信息，这可能导致我们无法均匀的散列散列值（素数：除了1和它本身以外不再有其他因数）

浮点数：将键表示为二进制数然后使用除留余数法（java就是这样做的）

字符串：除留余数法也可以处理较长的键，比如字符串，我们只需要将他们当做大整数就可以了，比如下面的代码就能用除留余数法计算String s的散列值

int hash = 0;    

for(int i=0; i<s.length(); i++){

	hash = (R*hash + s.charAt(i))%M;
}

java的charAt（）函数能够返回一个char值，即一个非负16位整数。如果R比任何字符的值都大，这个计算相当于将字符串当做一个N位的R进行制，将它除以M并且取余。一种叫Horner方法的经典算法用N次乘法，加法和取余来计算一个字符串的散列值。只要R足够小，不造成溢出，那么结果如我们所愿，落在0至M-1之内。使用一个较小的素数，如31，可以保证字符串中的所有字符都能发挥作用。

组合键：如果键的类型含有多个整型变量，我们可以和String类型一样将他们混合起来。例如被查找的键的类型是Data，其中含有几个整型的域：day（两个数数字表示的日），month（两个数字表示的月）和year（4个数字表示的年），我们可以这样计算它的散列值：

int hash = (((day * R + month) % M) * R + year) % M

只要R足够小不造成溢出，也可以得到一个0至M-1之间的散列值

Java的约定

每种数据类型都需要相应的散列函数，于是java令所有的数据类型都继承一个能够返回一个32比特整数的hashCode()方法。**每一种数据类型的hashCode（）方法都必须和equals（）方法一致。**也就是说，如果a.equals(b)返回true，那么a.hashCode()返回值必须和b的hashCode()的返回值相同。相反，如果两个对象的hashCode()方法返回值不同，那么两个对象是不同的。但如果，两个对象的hashCode()返回值相同，这两个对象也有可能不同，我们还需要用equals()方法进行判断。这就说明，如果你要为自定义的数据类型定义散列函数时，你需要重写equals()方法和hashCode()方法进行判断。默认的散列函数会返回对象的内存地址，但这只是使用于很少的情况。java为很多常用的数据类型重写了hashCode()方法（包括String,Integer,Double,File和URL）

将hashCode()的返回值转化成一个数组索引

因为我们需要的是一个数组的索引而不是一个32位的整数，我们在实现中会将默认的hashCode()方法和除留余数法结合起来产生一个0到M-1的整数，方法如下

private int hash(Key x){
	return (x.hashCode() & 0x7fffffff) % M;
}

这段代码会将符号位屏蔽（将一个32位整数变成一个31位非负整数），然后用除留余数法计算它除以M的余数。在使用这样的代码时我们一般会将数组的大小取M为素数以充分利用原散列值的所有位

自定义的hashCode()方法

散列表的用例希望hashCode()方法能够将键平均地散布为所有可能的32位整数，也就是说，对于任意对象x，可以调用x.hashCode()并认为有均等的机会得到一个2^32个不同整数中的任意一个32位整数值。Java中的String，Integer，Double，File和URL对象的hashCode()方法都能实现这一点。

32位计算机字长,用于表示整数,共有2的32平方个.所以,无符号整数的范围是0~2^32或0~4294967296带符号整数,因为需要1位来表示+-,所以范围为-2^31~2^31,或-2147483648~2147483648

软缓存

如果散列值的计算很耗时，那么我们可以将每个键的散列值缓存起来，即在每个键中使用一个hash变量来保存它的hashCode()的返回值。第一次调用hashCode()方法时，我们需要计算对象的散列值，但之后对hashCode()方法的调用会直接返回hash变量的值。

总之，要为一个数据类型实现一个优秀的散列方法需要满足三个条件:

一致性 - 等价的键必然产生相等的散列值

高效性 - 计算简便

均匀性 - 均匀地散列所有的键

基于拉链法的散列表

概念

散列算法的第二步是碰撞处理，也就是处理两个或者多个键散列值相同的情况。一种直接的方法就是将大小为M的数组中的每个元素指向一条链表，链表中的每个结点都存储了散列值为该元素的索引的键值对。这种方法叫做拉链法，因为发生冲突的元素都被存储在链表中。

基本思想

拉链法的基本思想就是选择足够大的M，使得所有的链表都尽可能短以保证高效的查找，查找分两步：首先根据散列值找到对应的链表，然后沿着链表顺序查找相应的键。

散列表的大小

在实现基于拉链法的散列表时，我们的目标是选择适当的数组大小M，既不会因为空链表而浪费大量内存，也不会因为链表太长而在查找上浪费太多时间。而拉链法的一个好处就是这并不是关联性的选择。如果存入的键多于预期，查找所需的时间只会比选择更大的数组稍长；如果少于预期，虽然有些空间浪费但查找会非常快。当内存不是很紧张时，可以选择一个足够大的M，使得查找需要的时间变成常数；当内存紧张时，选择尽量大的M仍然能够将性能提高M倍。

有序性相关的操作

散列最主要的目的在于均匀地将键散布开来，因此在计算散列后键的顺序信息就丢失了，如果是需要快速查找到最大或者最小的键，或者是查找某范围内的键，散列表都不是适合的选择，因为这些操作的运行时间都将会是线性的

但是基于拉链法的散列表的实现简单，在键的顺序并不重要的应用中，它可能是最快的（也是最广泛的）符号表实现，当使用Java内置数据类型作为键，或者是在使用含有经过完善测试的hashCode()方法的自定义类型作为键时，基于拉链法的散列表的算法能够快速而方便的查找和插入操作。

实现

/**
 * 基于拉链法的符号表
 * @author zzk
 *
 * @param <Key>
 * @param <Value>
 */
public class SeparateChainingHashST<Key, Value> {

	private static final int INIT_CAPACITY = 4;
	private int N; 	//键值对总数
	private int M;	//散列表的大小
	private SequentialSearchST<Key, Value>[] st; //存放链表对象的数组
	
	public SeparateChainingHashST(){
		this(997);
	}
	
	public SeparateChainingHashST(int N){
		//创建M条链表
		this.M = M;
		st = (SequentialSearchST<Key, Value>[]) new SequentialSearchST[M];
		for(int i=0; i<M; i++){
			st[i] = new SequentialSearchST(); 
		}
	}
	private int hash(Key key){
		return (key.hashCode() & 0x7fffffff)%M;
	}
	
	public Value get(Key key){
		return (Value)st[hash(key)].get(key);
	}
	//添加操作
	public void put(Key key, Value val){
		 if (key == null)
			throw new IllegalArgumentException("first argument to put() is null");
         if (val == null) {
            delete(key);
            return;
        }
         // double table size if average length of list >= 10
         if(N>=10*M)
        	 resize(2*M);
         
         int i = hash(key);
         if(!st[i].contains(key))
        	 N++;
		st[i].put(key, val);
	}
	//获取所有的键
	public Iterable<Key> keys(){
		Queue<Key> queue = new Queue<Key>();
		for(int i=0; i<M; i++){
			for(Key key : st[i].keys())
				queue.enqueue(key);
		}
		return queue;
	}
	//删除
	public void delete(Key key){
		if(key==null)
	      throw new IllegalArgumentException("argument to delete() is null");
		int i = hash(key);
		if(st[i].contains(key))
			N--;
		st[i].delete(key);
		
		//调整链表
		//保证查找效率
		if(M > INIT_CAPACITY && N <= 2*M)
			resize(M/2);
	}
	//动态调链表长度
	private void resize(int chains){
		SeparateChainingHashST<Key, Value> temp 
			= new SeparateChainingHashST<Key, Value>(chains);
		for(int i = 0; i < M; i++){
			for(Key key :st[i].keys()){
				temp.put(key, st[i].get(key));
			}
		}
		this.M = temp.M;
		this.N = temp.N;
		this.st = temp.st;
				
	}
	
}

基于线性探测法的散列表

概念

实现散列表的另一种方式就是用大小为M的数组保存N个键值对，其中M>N.我们需要依靠数组中的空位解决碰撞冲突。基于这种策略的所有方法统称为开放地址散列表。

开放地址散列表中最简单的方法叫做线性探测法：当碰撞发生时（当一个键的散列值已经被两一个不同的键占用），我们直接检查散列表中的下一个位置（将索引+1）。这样的线性探测会产生三种结果：

命中，该位置的键和被查找的键相同

未命中，键为空（该位置没有键）

继续查找，该位置的键和被查找的键不同

我们用散列函数找到键在数组中的索引，检查其中的键和被查找的键是否相同。如果不同则继续查找（将索引增大，到达数组结尾时折回数组的开头），直到找到该键或者遇见一个空元素，如图所示，我们习惯将检查一个数组位置是否含有被查找的键的操作叫做探测。等价于比较，不过有些探测实际上是在测试键是否为空

思想

开放地址类的散列表的核心思想是与其将内存作为链表，不如将他们作为在散列表的空元素。这些空元素可以作为查找结束的标志。

算法实现思路

分别将键和值保存在两个数组中，使用空（标记为null）来表示一簇键的结束（算法在添加键值时，如果key值对应的位置已有元素，那么会在元素的下一位继续寻找插入位置，直到找到位置插入，由此会在数组中形成一连续的条目，叫做键簇）。如果一个新建的散列值是一个空元素，那么就将它保存在那里；如果不是，就顺序查找一个空元素来保存它。如果要查找一个键，就从它的散列值开始顺序查找。如果找到就命中，如果遇见空元素则未命中。如果要删除一个键,删除key值以及对应的value,然后对于key后面的元素进行重新put，并且动态改变数组的大小.

实现

/**
 * 
 * 基于线性探测的符号表
 * @author Administrator
 *
 * @param <Key>
 * @param <Value>
 */
public class LinearProbingHashST<Key, Value> {
	
	private int N;  //符号表中的键值对的总数
	private int M = 16; //线性探测表的大小
	private Key[] keys; //键
	private Value[] vals;//值
	public LinearProbingHashST(){
		keys = (Key[]) new Object[M];
		vals = (Value[]) new Object[M];
	}
	private int hash(Key key){
		return (key.hashCode() & 0x7fffffff) % M;
	}
	
	//调整数组大小(调大或者调小)
	private void resize(int cap){
		LinearProbingHashST<Key, Value> t;
		t = new LinearProbingHashST<Key, Value>();
		for(int i=0; i<M; i++){
			if(keys[i]!=null){
				t.put(keys[i], vals[i]);
			}
		}
		keys = t.keys;
		vals = t.vals;
		M  = t.M;
	}
	
	//添加键值（如果key值对应的位置已有元素，那么会在元素的下一位继续寻找插入位置）
	private void put(Key key, Value val){
		if(N>=M/2)
			resize(2*M);//将M加倍
		int i;
		for(i=hash(key); keys[i]!=null; i = (i+1)%M){
			if(keys[i].equals(key)){
				vals[i] = val;
				return;
			}
		}
		keys[i] = key;
		vals[i] = val;
		N++;
	}
	//获取值（如果key所在位置为null，那么不存在，如果所在位置key不相等，那么会继续下移找下一个key）
	public Value get(Key key){
		for(int i=hash(key); keys[i]!=null; i = (i+1)%M){
			if(keys[i].equals(key)){
				return vals[i];
			}
		}
		return null;
	}
	//获取所有的键
	public Iterable<Key> keys(){
		Queue<Key> queue = new Queue<Key>();
		for(int i=0; i<M; i++){
			if(keys[i]!=null)
				queue.enqueue(keys[i]);
		}
		return queue;
	}
	//删除操作（删除key值以及对应的value,然后对于key后面的元素进行重新put，并且动态改变数组的大小）
	public void delete(Key key){
		if(!contains(key))
			return;
		int i = hash(key);
		while(!key.equals(keys[i])){
			i = (i+1)%M;
		}
		//删除指定的位置数
		keys[i] = null;
		vals[i] = null;
		
		i = (i+1)%M;
		while(keys[i]!=null){
			Key keyToRedo = keys[i];
			Value valTpRedo = vals[i];
			keys[i] = null;
			vals[i] = null;
			N--;
			put(keyToRedo, valTpRedo);
			i = (i+1)%M;
		}
		N--;
		//保证所用的内存量和表中的键值对的比例总在一定范围之内，动态调整数组大小保证N/M不大于1/2
		if(N>0 && N<=M/8)
			resize(M/2);
	}
	//判断是否存在key值
	public boolean contains(Key key){
		if(key==null)
			throw new IllegalArgumentException("argument to contains() is null");
		return get(key)!=null;
	}
}

线性探测法的性能

当散列表快满时，查找所需的探测次数是巨大的（N(插入元素数量)/M（数组大小）趋近于1，探测的次数也越来越大），但是当使用率（N/M）小于1/2时探测的预计次数只在1.5到2.5之间，所以可以通过动态调整数组的大小来改变性能。

在每一次插入新建时，会进行判断N(插入元素数量)是否大于1/2M（数组大小），如果是，动态调大数组大小M，即扩大到2*M，从而保证每一次插入，散列表最多半满状态。

而对于删除操作，在最后要加上如果N>0 && N<=M/8,M要改变成M/2,一直保证N/M不大于1/2,保证查找效率

拉链法的性能

对于拉链法也可以进行调整，在拉链法中保持较短的链表（平均长度在2到8之间），也就是1/4~N/M<1~1/2，在进行新建插入操作时，当N>=8M时，也就是N刚好差不多接近1/2M，所以M要变成2M，保证插入后N/M不大于1/2，进行删除操作，删除完毕后，判断N>0 && N<=2M,要调整成M/2，调小N/M，提高查找效率。